排列组合

排列 permutation（arrangement） 和组合 combination 纯粹的数学上的排列组合的定义是

  • 排列 就是指从给定 n 个数的元素中取出指定 r 个数的元素，进行排序
  • 组合 从给定 n 个数的元素中仅仅取出指定 r 个数的元素，不考虑排序

排列与组合唯一的区别在于操作元素的顺序是否影响了统计的结果。

数学中常用到的排列组合的公式主要用来统计目标个数。

回溯法

在一些常见的算法问题中，有时候是需要输出期望的子集合。这个时候就需要采用回溯的方式来解决。

维基百科的定义是

回溯法（英语：backtracking）是暴力搜索法中的一种。
对于某些计算问题而言，回溯法是一种可以找出所有（或一部分）解的一般性算法，尤其适用于约束满足问题（在解决约束满足问题时，我们逐步构造更多的候选解，并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜索这个部分候选解本身及其可以拓展出的子候选解，转而测试其他的部分候选解）

给定一个没有重复数字的序列，返回其所有可能的全排列（原题）。如

1
2
3
4
5
6
7
8
9
10
11
12
Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

在有 3 个元素的序列中，子序列的个数可以分别为 0，1，2，3 四种。本质上回溯法是 DFS，这个问题也就演变成了一个遍历树的思路。

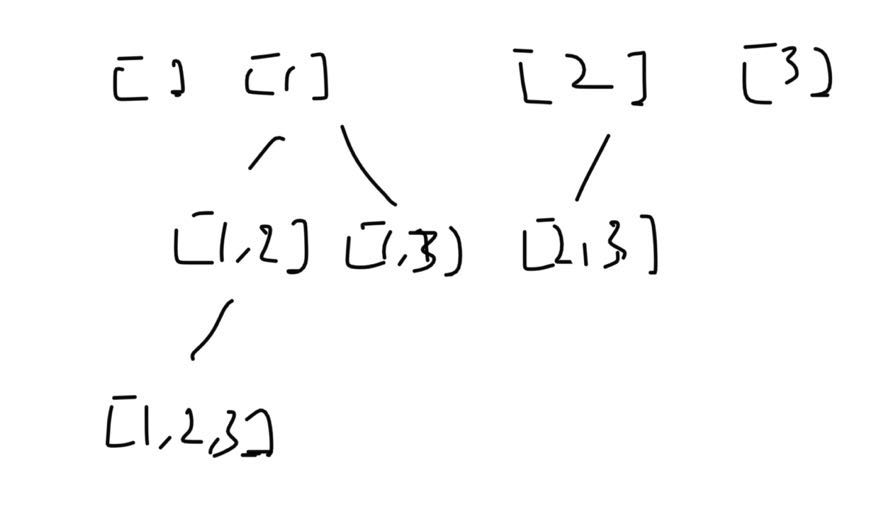
subset

1
2
3
4
5
6
7
8
 void backtrack(List<List<Integer>> list , List<Integer > tempList, int [] nums, int start){
    list.add(new ArrayList<>(tempList));
    for(int i = start; i < nums.length; i++){
        tempList.add(nums[i]);
        backtrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);  // 注意回溯的时候需要删掉最后一个，保证用下一个元素取替换并继续递归
    }
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> list = new ArrayList();
        Arrays.sort(nums);
        backTrack(list, new ArrayList(), nums, 0);
        return list;
    }

private void backTrack(List<List<Integer>> list, List<Integer> tempList, int[] nums, int start) {
    list.add(new ArrayList(tempList));
    for (int i = start; i < nums.length; i++) {
        tempList.add(nums[i]);
        backTrack(list, tempList, nums, i + 1);
        tempList.remove(tempList.size() - 1);
    }
}