N 皇后问题是最早一位棋手提出了八皇后问题之后，推演而来的。八皇后问题的规则是：

  • 在 8 * 8 的盘中放置 8 个皇后
  • 任何一个皇后的横，竖，斜对角都不能别的皇后

我们要从中找到尽可能多的摆放方法。下图是解法之一

八皇后问题
八皇后问题

随后，这个问题被推演成为了 N 皇后问题。也就是当棋盘大小为 N（N > 0），皇后个数为 N 的时候，有多少种摆放方法。目前前 10 个分别是

1
2
3
4
5
6
7
N => [1, 2, 3, 4, 5,  6, 7,  8,  9,   10]
U => [1, 0, 0, 1, 2,  1, 6,  12, 46,  92]
D => [1, 0, 0, 2, 10, 4, 40, 92, 352, 724]

# N 棋盘大小
# U 不包括对称的解
# D 包括了对称的解

注意到六皇后问题的解的个数比五皇后问题的解的个数要少。现在还没有已知公式可以对 n 计算 n 皇后问题的解的个数，也就是说这个问题现在还只能由程序来解答。

核心的思路是：给棋盘定义坐标，比如左上是（0，0）横轴为 x 竖轴 为 y。如果抽象成为一个二维数组，x 和 y 就是数组元素的 index。当一个皇后落子之后，那么相对应的所有 x 和 y 以及对角线就都不能下这里被称为控制区域。也就是当一个皇后（坐标为 x，y）落子之后那么棋盘的 colomns[x] 和 rows[y] 以及对角线就都被控制。

这里最先想到的是每个位置遍历，总共记录 n^2 个位置。不过这一步可以精简为记录历行，因为我们知道一行如果落子了就不在考虑这一行。也就是说如果从 0 开始往棋盘的下方遍历，那么落子之后只需要记录这一列是否下过即可。用 colomns[x] 来表示这一列。

对于对角线，一个 8 * 8 的棋盘中对角线的个数是 15 个 / + 15 个 \。这个很容易推算，对于一个标准的 n * n 棋盘，单个方向的对角线个数

diag = 2 * n - 1

也即是说对角线是否被控制可以用对角线的数组表示。假设 / 是 diag1， \ 是 diag2。

那么又有一个问题了，一个落子所控制的对角线能否被找到呢。比如说落在 (x, y) 处在，那么是否能找到对应的 diag1 和 diag2 呢？答案是可以的。 至于如何推算的，画一下图就知道啦。

  • 对于 /，对应的是 diag1[x + y]
  • 对于 \，对应的是 diag1[x - y + n - 1]

至此，落子之后控制区域如何表示就没有问题了。

接下来就是探究怎么找到所有的落子。本质上这是一个典型的回溯法。

作为回溯算法的一种，自然是用树形空间来表示递归。例如当 n = 4 的时候，搜索空间可以用一颗 4 叉树来表示

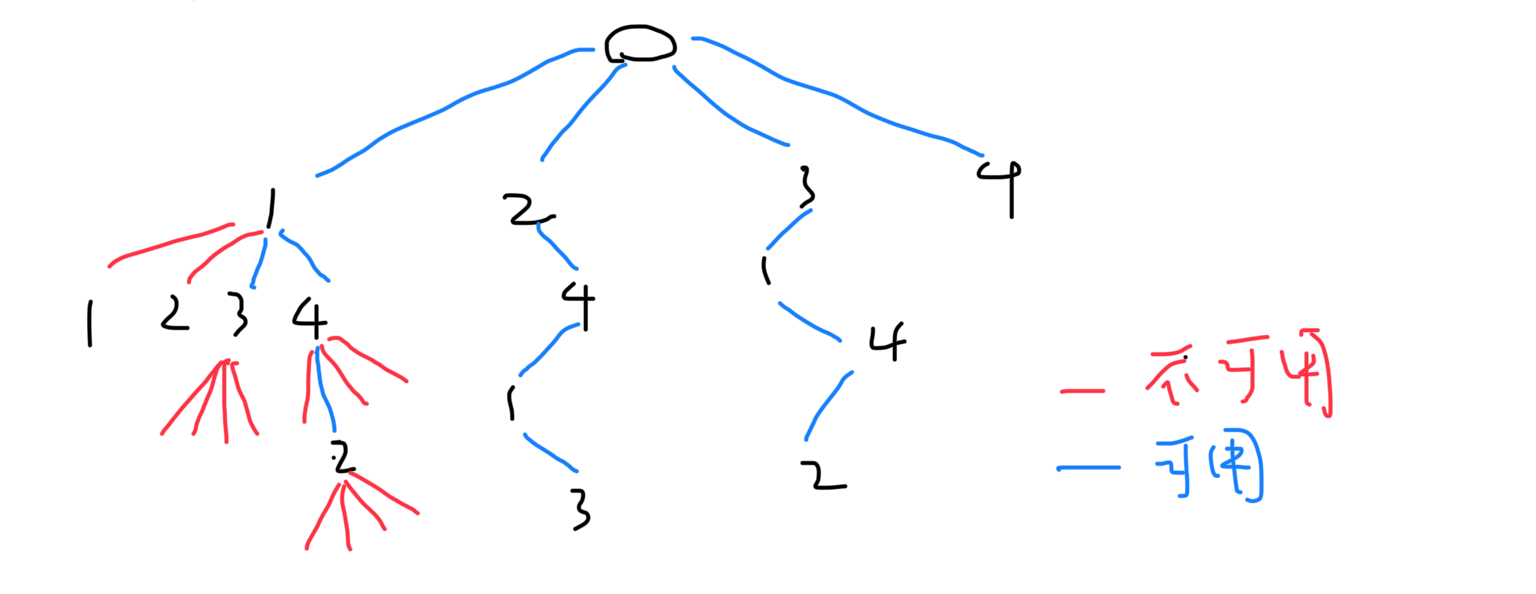
首先从 0 开始遍历棋盘的 x 轴。并在此基础上，递归地寻找后面的位置。递归期间可以落子，那么就放入棋盘，同时更新控制的区域，继续递归。当发现递归到树的底层，或者说后面的节点全都不能遍历的时候回溯。反之，就继续遍历。

这种的典型的多插树搜索很大程度基本的递归结构是

1
2
3
4
# 伪代码
def recur()
  for i in range
   recur()

树的节点个数通常是 range 的大小， recur 的深度是树的深度。

那么至此可以开始设计这个 leetcode 上难度为 hard 的题目 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public class Solution {
    private List<String> board;
    private boolean[] cols;
    private boolean[] diag1;
    private boolean[] diag2;
    private List<List<String>> solution;

    public List<List<String>> solveNQueens(int n) {
        solution = new ArrayList<>();
        board = new ArrayList<>();
        char[] charArray = new char[n];
        Arrays.fill(charArray, '.');
        for (int i = 0; i < n; i++) {
            board.add(new String(charArray));
        }
        cols = new boolean[n];
        diag1 = new boolean[2 * n - 1];
        diag2 = new boolean[2 * n - 1];
        nQueens(n, 0);
        return solution;
    }

    private void nQueens(int n, int y) {
        if (y == n) {
            solution.add(new ArrayList<>(board));
            return;
        }

        for (int x = 0; x < n; x++) {
            if (!available(x, y, n)) continue;
            updateBoard(x, y, n, true);
            nQueens(n, y + 1);
            updateBoard(x, y, n, false);
        }
    }

    private boolean available(int x, int y, int n) {
        return !cols[x] && !diag1[x + y] && !diag2[x - y + n - 1];
    }

    private void updateBoard(int x, int y, int n, boolean put) {
        cols[x] = put;
        diag1[x + y] = put;
        diag2[x - y + n - 1] = put;
        char[] columns = board.get(y).toCharArray();
        columns[x] = put ? 'Q' : '.';
        board.set(y, new String(columns));
    }
}

附: 完整的代码&测试用例