给出两个单词 word1 和 word2，找出把 word1 编辑成 word2 的最短编辑距离。给出的可用编辑操作有：

  1. 插入一个字符 insert
  2. 删除一个字符 delete
  3. 更新一个字符 update

编辑距离是针对二个字符串（例如英文字）的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。编辑距离可以用在自然语言处理中，例如拼写检查可以根据一个拼错的字和其他正确的字的编辑距离，判断哪一个（或哪几个）是比较可能的字。DNA也可以视为用A、C、G和T组成的字符串，因此编辑距离也用在生物信息学中，判断二个DNA的类似程度。Unix 下的 diff 及 patch 即是利用编辑距离来进行文本编辑对比的例子。

传送门

对于 “a”, “”, 执行步骤 1
对于 “”, “a”, 执行步骤 2
对于 “a”, “b”, 执行步骤 3

假设字符串串 word1 和 word2 的最小编辑距离是 d[i][j] (i 和 j 代表 word1 和 word2 的长度 - 1)，当我们给 word1 和 word2 都 append 一个相同的字符的时候，这个编辑距离不变。因此可以认为，此时的 d[i+1][j+1] == d[i][j]。当 append 的字符不同的的时候。就是找到之前的最小编辑距离 + 1，这个之前的最小编辑距离可能是 d[i][j]、d[i][j+1]、或者 d[i+1][j]。

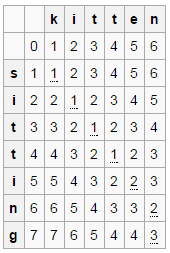
Edit-Distance.png
Edit-Distance.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minDistance(String word1, String word2) {
        if (word1 == null || word2 == null) return 0;
        
        int m = word1.length() + 1, n = word2.length() + 1; //多的一行留给空字符串
        
        int[][] d = new int[m][n];
        
        for (int i = 0; i < m; i++)
            d[i][0] = i;
        for (int j = 0; j < n; j++)
            d[0][j] = j;
        
        for(int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (word1.charAt(i-1) == word2.charAt(j-1))
                    d[i][j] = d[i-1][j-1];
                else
                    d[i][j] = min(d[i-1][j-1], d[i][j-1], d[i-1][j]) + 1;
            }
        }
        return d[m-1][n-1];
                
    }
    
    private int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}