Scala 函数式编程设计

在这个 2020 年初的特殊时期。

Scala 是一门现代化，多范式的 JVM 语言。

传送门（可能需要🚀)

W1

case class 和模式匹配

用 Scala 来表示 JSON 对象可以这样

abstract class JSON
case class JSeq (elems: List[JSON]) extends JSON  // JSON 的数组
case class JObj (bindings: Map[String, JSON]) extends JSON // JSON 对象
case class JNum (num: Double) extends JSON // 数字类型
case class JStr (str: String) extends JSON
case class JBool(b: Boolean) extends JSON
case object JNull extends JSON // 空

所以，

{
    "firstName" : "John",
    "lastName" : "Smith",
    "address" : {
        "streetAddress" : "21 2 nd Street",
        "state" : "NY",
        "postalCode": 10021
    },
    "phoneNumbers": [
        {"type" : "home","number ": "212 555 -1234"} ,
        {"type" : "fax","number ": "646 555 -4567"}
    ]
}

可以表示为

val data = JObj(Map(
    "firstName" -> JStr("John"),
    "lastName" -> JStr("Smith"),
    "address" -> JObj(Map(
    "streetAddress" -> JStr("21 2nd Street"),
    "state" -> JStr("NY"),
    "postalCode" -> JNum(10021)
)),
"phoneNumbers" -> JSeq(List(
    JObj(Map(
    "type" -> JStr("home"), "number" -> JStr("212 555-1234")
)),
JObj(Map(
    "type" -> JStr("fax"), "number" -> JStr("646 555-4567")
)) )) ))

比如说我要实现一个打印 JSON 对象的方法，就可以

def show(json: JSON): String = json match {
    case JSeq(elems) =>
    "[" + (elems map show mkString ", ") + "]"
    case JObj(bindings) =>
    val assocs = bindings map {
        case (key, value) => "\"" + key + "\": " + show(value)
    }
    "{" + (assocs mkString ", ") + "}"
    case JNum(num) => num.toString
    case JStr(str) => '\"' + str + '\"'
    case JBool(b) => b.toString
    case JNull => "null"
}

上述的 show(data) 就输出

res1: String = {"firstName": "John", "lastName": "Smith", "address": {"streetAddress": "21 2nd Street", "state": "NY", "postalCode": 10021.0}, "phoneNumbers": [{"type": "home", "number": "212 555-1234"}, {"type": "fax", "number": "646 555-4567"}]}

第 6 行代码里面 map 传入的函数是，我们知道，在这里 map 函数的签名是 def map[B](f: (A) => B): List[B]
那么第六行的 f 就是 case (key, value) => "\"" + key + "\": " + show(value)。这个函数如果单独拎出来，其实就是

1	val f: (String, JSON) => String = { case (key, value) => key + ”: ” + value } // 注意看 JObj 定义

所以用 case class 最方便的地方在于模式匹配中的 decompose

函数即对象

任何情况下，函数 A => B 其实就是

1	scala.Function1[A, B]

的简写。

普通函数

根据 Function1 的定义

1
2
3

trait Function1[-A, +R] {
    def apply(x: A): R
}

例如，

1 2	val f1: Int => Int = (x: Int) => x + 1 val f2 = new Function1[Int, Int] {def apply(x: Int) = x + 1}

f1 和 f2 等价。

偏函数

对于偏函数 PartialFunction 定义为

trait PartialFunction[-A, +R] extends Function1[-A, +R] {
    def apply(x: A): R
    def isDefinedAt(x: A): Boolean
}

例如，

val f1: PartialFunction[String, String] = { case "ping" => "pong" }
val f2 = new PartialFunction[String, String] {
    def apply(x: String) = x match {
        case "ping" => "pong"
    }
    def isDefinedAt(x: String) = x match {
        case "ping" => true
        case _ => false
    }
}

f1 和 f2 等价。

ps: 以上，「等价」的意思是两个函数只要输入相同，输出一定相同。

W2

LazyList

下面代码

def f(x: Int): Boolean = {
  println(x + " ")
  x % 11 == 0
}

val v1 = (1 to 100000).filter(f)(1)
val v2 = (1 to 100000).to(LazyList).filter(f)(1)

v1 和 v2 等价。计算 v1 的时候会打印 1 2 3...9999 100000, 而计算 v2 的时候打印 1 2 3 ... 21 22。这是因为对于 v2，(1 to 100000).to(LazyList) 产生的是 scala.collection.immutable.LazyList。其中官方文档对其有个简单的描述

This class implements an immutable linked list that evaluates elements in order and only when needed

也就是当 LazyList 里面的元素被需要的时候，才会进行有序计算，并且计算会终止知道所需的元素计算结束。这也就是为什么会有上述的输出了。

惰性求值 Lazy Evaluation

在 Scala 里面，Lazy 意味着两点

尽量延后求值计算
只计算一次

例如

def expr = {
  val x = { print(”x”); 1 }
  lazy val y = { print(”y”); 2 }
  def z = { print(”z”); 3 }
  z + y + x + z + y + x // last line
}
expr

这样的输出为 xzyz

Infinite Sequences

利用 LazyList 的特性，可以构造出无限序列。比如

scala> def from(n: Int): LazyList[Int] = n #:: from(n + 1) // 无限序列
from: (n: Int)LazyList[Int]

scala> val natures = from(0) // 自然数
natures: LazyList[Int] = LazyList(<not computed>)

scala> val hundreds = natures.filter(_ % 100 == 0)
hundreds: scala.collection.immutable.LazyList[Int] = LazyList(<not computed>)

scala> val fourHundred = hundreds(4) // 计算
fourHundred: Int = 400

埃拉托斯特尼筛法

埃拉托斯特尼筛法是列出所有小素数最有效的方法之一，其名字来自于古希腊数学家埃拉托斯特尼，并且被描述在另一位古希腊数学家尼科马库斯所著的《算术入门》中。-维基百科

用 LazyList 实现会非常简单，

def from(n: Int): LazyList[Int] = {
  n #:: from(n + 1)
}

def sieve(s: LazyList[Int]): LazyList[Int] = {
  s.head #:: sieve(s.tail.filter(_ % s.head != 0))
}

def primeNumber(n: Int): Int = {
    sieve(from(2))(n)
}

val n = sieve(from(2))(100) // 输出 547

题目：倒水问题

给几个知道容量，但是没有刻度的杯子，有个可以取之不尽的水源用来给杯子装满水和将杯子的水全部倒出。我们需要做的就是盛出给定容量的水。我们能做的操作有三个

empty 清空
fill 放满水
pour(a, b) 把 a 的水全部往 b 倒直至 b 杯满了或者 a 杯没水了

现在需要找到取得容量为 N 的水时，需要的操作。

附：1. Scala 完整代码 2. python 解法

W3

下面会用 Scala 进行加法器模拟。对于计算机中，两个数如何相加，可以提前阅读维基百科-加法器，最好能够做一下位运算实现加法。

通过以上内容，我们需要知道的最重要的点在于：两个一位二进制数相加，将会产生两个输出，其中一个是当前位相加的值 S，另一个是相加后的进位信息 C。其中 S 可以用异或门，进位可以用与门。两个半加器用或门组合为一个全加器。

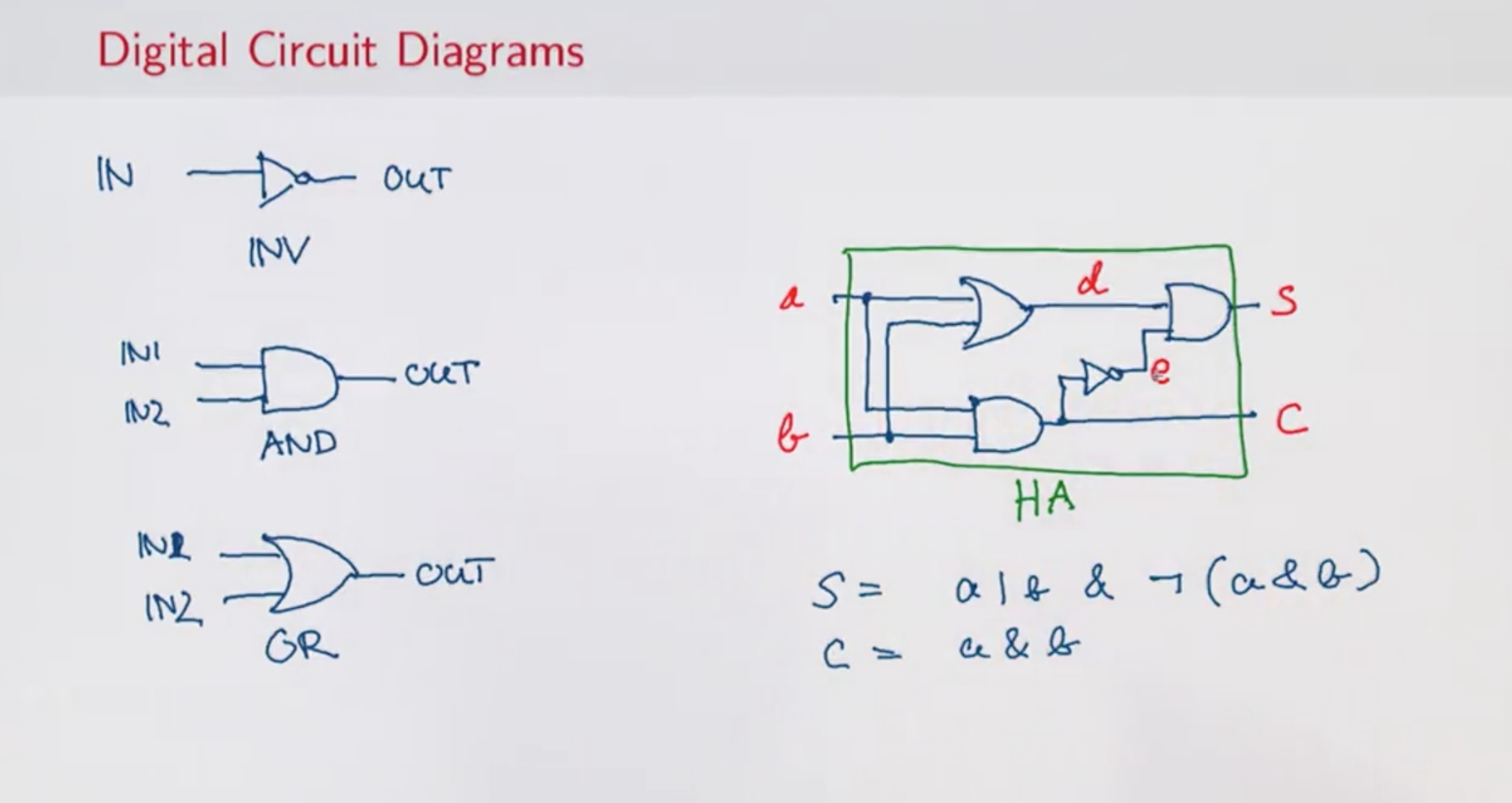
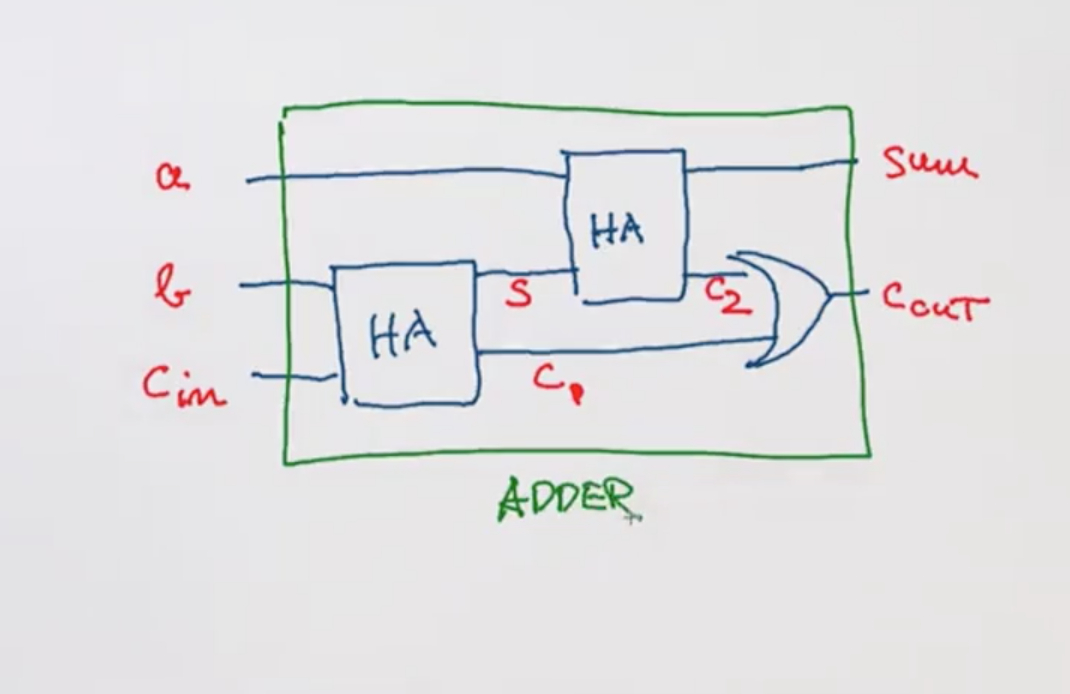
根据上图，我们至少需要实现的是

电线：用来传导信号，信号可以用 boolean 类型表示 0 和 1

class Wire {
  private var sigVal = false
  def getSignal: Boolean = sigVal
  def setSignal(s: Boolean): Unit =
    if (s != sigVal) {
        sigVal = s
        actions foreach(_())
    }
}

与门：输入两个电信号，输出 & 对应的信号

1	def andGate(in1: Wire, in2: Wire, output: Wire): Unit = ???

或门：输入两个电信号，输出 | 对应的信号

1	def orGate(in1: Wire, in2: Wire, output: Wire): Unit = ???

逆变器：输入电信号，输出 ! 对应的信号

1	def inverter(in: Wire, output: Wire): Unit = ???

在此基础上，实现出半加器和全加器

def halfAdder(a: Wire, b: Wire, s: Wire, c: Wire): Unit = {
  val d = new Wire
  val e = new Wire
  orGate(a, b, d)
  andGate(a, b, c)
  inverter(c, e)
  andGate(d, e, s)
}

def fullAdder(a: Wire, b: Wire, cin: Wire, sum: Wire, cout: Wire): Unit = {
  val s = new Wire
  val c1 = new Wire
  val c2 = new Wire
  halfAdder(b, cin, s, c1)
  halfAdder(a, s, sum, c2)
  orGate(c1, c2, cout)
}

实现了全加器后。加入模拟信号的输入输出即可，完整代码模拟加法器

W4

Functional Reactive Programming (FRP)

在 MVC 模型中，FRP 可以让 model 在产生变化的同时 view 自动变化。这样的模型一般也就是 pub-sub 模型或者叫观察者模型 (observers)。

Subscriber1   subscribe     ___________
Subscriber2  ------------> |          |
Subscriber3                |Publisher |
Subscriber4  <------------ |          |
Subscriber5    publish     |__________|

通用的说比如 a = f(b) 里面。当 b 在发生变化的时候 a 也会跟着变。实现这一点，
可以把「变化」归化为「event」，而自动检查这些「event」的东西叫做 Signal。在 Scala 里面通常把这样的 Signal 实现为一个类型，通过 apply() 给其赋值。比如

1 2	val s = Signal(1) val v = s() // 1

同时，为了给 Signal 再次赋值，可以扩展新增一个 update 方法。比如 s.update(5)，顺带可以写成 s() = 5。这样的话，实现一个扩展了 Signal 名为 Var 的类型，让其拥有 update 方法。

在这样的条件下，

// (1)
val num = Var(1)
val twice = Signal(num() * 2)
num() = 2
// (2)
var num = Var(1)
val twice = Signal(num() * 2)
num = Var(2)

(1) 里面的 twice 变为 4，（2）里面的 twice 还是 2。上述体现的 FRP 里面，num 是 publisher，twice 是 subscriber。num 产生了 event，twice 接受这样的 event。并且所有的变量本身都是 immutable。

实现 FRP

Var 和 Signal

我们知道 Signal 和 Var 应该是这样

// signal
class Signal[T](expr: => T) {
    def apply(): T = ???
}

object Signal {
  def apply[T](expr: => T) = new Signal(expr)
}

// var
class Var[T](expr: => T) extends Signal[T](expr) {
    def update(expr: => T): Unit = ???
}
object Var {
    def apply[T](expr: => T) = new Var(expr)
}

维护订阅关系

有了这些方法，就可以做到赋值和再次赋值。还需要的是，当一个 publisher 产生了 event 的时候，如何自动通知到对应的 subscriber，并且让其重新计算（re-evaluate）。

例如，s 是 Var 类型，并且进入到了表达式 expr 里，形如 expr s，那么当表达式 expr s，作为参数传递给了某个 Signal 形如 val t = Signal(expr s) 的时候。就需要给 s 维护一个 subscriber。同理，当有多个 subscribers 的时候就给 s 维护一个 subscriber 的集合。比如

// val set = Set()
var num = Var(1)

// 触发的条件就是 class Var 的 apply 方法。

// 触发：set += Signal(num() * 2)
val double = Signal(num() * 2)

// 触发：set += Signal(num() * 3)
val tiple = Signal(num() * 3)

触发的条件达到了，可是如何把 Signal(num() * 3) 这样的对象传递给 num 的 set ？

这个时候就需要在 Object Signal 里面新增一块用于维护方法调用的数据结构，没做就是 stack

object Signal {
  val caller = new StackableVariable[Signal[_]](NoSignal)
  def apply[T](expr: => T) = new Signal(expr)
}

StackableVariable 在当前的上下文中多个 Signal/Object 会共享。当调用 class Signal 的 apply() 方法的时候就去这里面找到当前的调用方。

维护调用栈

调用栈里面存放有序的 Signal。例如，有下面测试代码

test("multi subscribers") {
  val publisher = Var(1)
  val subscriber1 = Signal(publisher() * 20) // 注意 scala 的 call-by-name 和 call-by-value。这里传递的是表达式
  val subscriber2 = Signal(publisher() * 30)
  val subscriber3 = Signal(publisher() * 40)
  assert(subscriber1() == 20)
  assert(subscriber2() == 30)
  assert(subscriber3() == 40)
  publisher() = 2
  assert(subscriber1() == 40)
  assert(subscriber2() == 60)
  assert(subscriber3() == 80)
}

第三行开始，包含表达式的 Signal 进入调用栈，并不断被带入 subscriber 的集合。

class StackableVariable[T](init: T) {
  private var values: List[T] = List(init)

  def value: T = values.head

  def withValue[R](newValue: T)(op: => R): R = {
    values = newValue :: values
    try op finally values = values.tail
  }
}

完整代码